thesephist.com

Notational intelligence

2 January 2022
2 Jan 2022
New York, NY
32 mins

I spent the last month wondering and investigating how we might design better workflows for creative work that meld the best of human intuition and machine intelligence. I think a promising path is in the design of notation. More explicitly, I believe inventing better notations can contribute far more than automated tools to our effective intelligence in understanding ourselves, the world, and our place in it.

This post is on the longer side (it’s really three essays in one), so we begin with a roadmap. Feel free to skip around.

  1. A brief tour of notational diversity
  2. Interpreting intelligence
  3. Notational intelligence
  4. Future directions

To understand good notation and its role in knowledge work, we must first begin with a brief tour of notation in all its beautiful variety.

Part One: A brief tour of notational diversity

Notation, like its conceptual cousin language, is difficult to define precisely because it covers such a wide range of ideas. But as a starting point, let’s constrain notation to be some arrangement of symbols or images that we use to record and communicate ideas, and the way we interact with those symbols in our thinking process.

The most widely used and influential notation is writing systems for natural languages. It’s tempting to imagine spoken and written language as two sides of the same coin, but writing down spoken language changes our relationship to language and to our ideas. Spoken language is useful for communicating in small groups, and perhaps for thinking aloud. When we write ideas down, we make those ideas durable and reliable through time. This difference also delineates the shift from oral to written tradition in history. All of science, all of literature, all of trade and politics are built on top of the fact that we can write down an idea, and expect it not to change over time. When we record events in writing, we can have a coherent idea of facts as something separate from simply what we say, which might fade with our memories. Ted Chiang articulates the power of written language beautifully in Truth of Fact, Truth of Feeling:

Writing was not just a way to record what someone said; it could help you decide what you would say before you said it. And words were not just the pieces of speaking; they were the pieces of thinking. When you wrote them down, you could grasp your thoughts like bricks in your hands and push them into different arrangements. Writing let you look at your thoughts in a way you couldn’t if you were just talking, and having seen them, you could improve them, make them stronger and more elaborate.

The strength of writing demonstrates a common strength of all notations, which is to take something abstract, like the concept of “thought”, and make it concrete, into marks on paper or ink on a page. You can arrange thoughts and ideas into shapes and lists in writing, in a way that isn’t possible when thoughts turn into vapor the moment they are spoken aloud. With writing, I can hold onto ideas over time and refer back to them, unencumbered by the anemic limits of my brain. I can send them to a million people and trust that they will all read exactly what I had spoken within my own mind. This property of notation as embodied abstraction will appear many times throughout the rest of this post.

In contrast to the expressive flexibility of language, mathematical notation derives its strength from its rigidity and precision.

Math notation is really a family of conventions that are used together in practice to communicate quantitative ideas. Some of the greatest hits from this collection include:

Math notation is a powerful demonstration of how good (and bad) design of notation can make certain kinds of thinking trivial or impossibly difficult. The reason for this goes back to our earlier lesson from written language: good notation gives us the ability to work work abstract concepts (like sets or infinities) using the same cognitive muscles we use to work with physical objects, as concrete, embodied objects in our visual and tactile world. Because of this I think it’s helpful to think of the notation we use to represent ideas not just as simple tools, but as an integral part of how we think.

We think in languages; we think with notations.

Given that notation is so important to shaping our thinking, what properties might we want in a good notation? Mathematician Terence Tao muses on some desirable properties of good notation here. He begins by noting that a notation is only meaningful in the context of some domain of work. The symbol “IV” means something completely different in arithmetic than it does in cryptography or music theory. With that in mind, he emphasizes these properties (among others):

Because of the versatility and precision of math notation, it has found widespread adoption in related fields like engineering, statistics, and computer science. Math notation in those fields often look slightly different (for example, in computer science, variables are often words, not single letters), but they adopt the basic principles above, like using letters to represent unknown quantities, or using a single symbol to represent a set of things.

For more esoteric stories of notational revolution in the way we work, we can turn to dance and other physical activities like juggling.

Dance notation, using Zorn notation. By Huster at French Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4360733

– Dance notation, using Zorn notation. From French Wikipedia, CC BY-SA 3.0

These domains had suffered for a long time from the difficulty of representing complex choreographies on paper. How do you write down even a short choreography onto paper in a way that would be precisely and unambiguously read back by a stranger? There have been countless attempts across history to invent better notations for representing dance and juggling – some of them have even led to invention of new moves or juggling patterns. More recently, cheap and easy sharing of video has revolutionized how practitioners communicate their motion. Compared to learning the notations and practicing reading back symbols from paper, it’s much easier to watch a dance video and follow along. Video is much more expressive, and also much less ambiguous. I think it’s fair to say video would be a promising medium for a new dance notation.

Our last example of classic notations lies in western music tradition: music notation. This notation is the total sum of the way modern composers and songwriters write music to be read back by performers or arrangers. Just like math notation, there are a few key concepts: the five-line staff, key signatures and notes, dynamics, and so on. But composers and instrumentalists might also use special notation to represent unconventional instructions (like humming, clapping, bowing styles for string instruments). Like language, music notation stretches to become as expressive as we need it to be.

Chaotic, hand-written music notation. Sourced from https://twitter.com/ThreatNotation/status/1464807856511852552

– Questionable use of music notation, from @ThreatNotation on Twitter

As in dance and juggling, many performers are augmenting music notation with digital video and audio. Modern musicians might reference a YouTube recording of a world-class performer to help them understand nuances in tone that notation doesn’t quite capture, and vocal artists might reference demo tracks to remember exactly how they want to deliver certain lines without having to write down every modulation of tone in their performance.

Neither math nor music notation is easy to learn, but every practitioner learns them to reap the benefits of thinking in the notation, using the abstractions they provide. I think it’s worth noting that ease of learning is not a necessary property of good notation. This is because learning a new notation often involves learning to think with entirely new basic concepts. As long as the notation embodies useful concepts, the difficulty of learning it is vastly outweighed by the ease of thinking using those concepts once the notations feel natural to use.

Beyond these popular notations, there are specialized notations for every niche and field out there. My favorite example is the fishbone lab diagram used in medicine to record measurements concisely. There are notations used in screenwriting and theater, notations for describing electrical circuits, for professional copy editing, and on and on. Wikipedia has an even longer list of lesser-known notation. Humans invent notation whenever and wherever we need to work with common abstractions. Along with our ability to use tools, our ability to invent notation might be a defining characteristic of human intelligence. (Ken Iverson would probably say notations are tools, but here, I want to make a finer distinction between tools we use to manipulate physical objects, and notations we use to represent abstract ideas.)

Computable notation

With the advent of stored-program computers, humanity was presented with an entirely new class of notation: notation that can be executed. I use the phrase computable notation to describe this group.

The most obvious example of computable notation is programming languages. Programming languages inherit many desirable traits of natural language writing systems, like words representing distinct concepts and grammars to describe syntactically valid expressions. The main strength of programming languages is that they can be evaluated mechanically to accomplish a dizzying array of tasks. Programs can:

Despite these unique properties, programming languages are unquestionably notation first, and instructions second. If the notational qualities of programming languages were not important, we would all just write code in assembly! Higher level languages let us work with new kinds of abstractions ergonomically, in the same way as any good notation. Which specific language we choose for a task depends on which languages give us the right symbols to represent useful concepts for that task.

One interesting programming language for our discussion of notation is Wolfram Language, the programming language used in Mathematica and WolframAlpha. Wolfram Language has a few unique advantages that makes it interesting as a powerful computational notation.

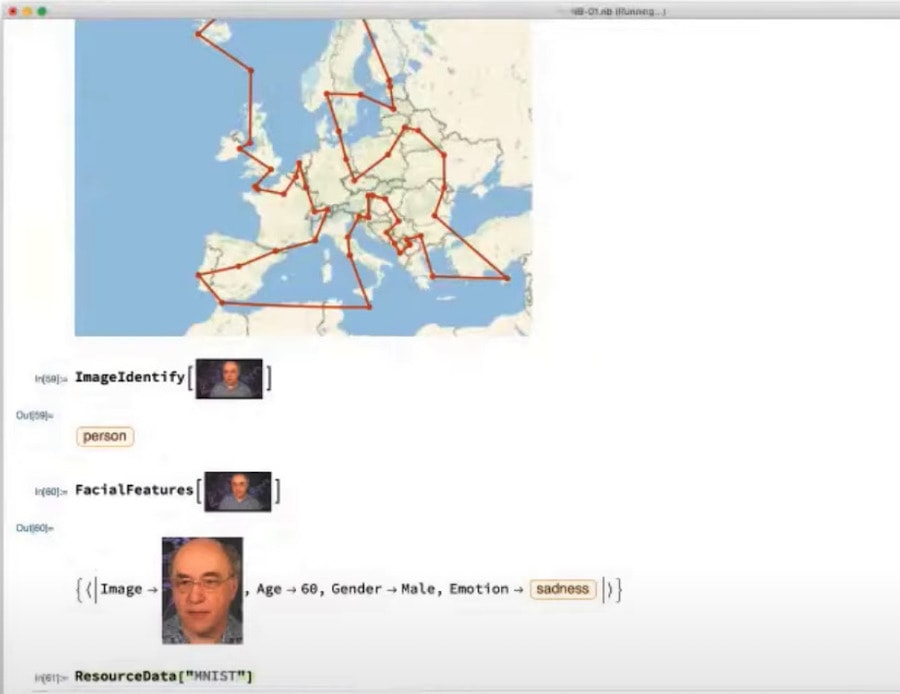
An interactive console running Wolfram Language, with image thumbnails interspersed into the programming syntax

– Wolfram Language working directly with images as a first-class part of its notation, sourced from Stephen Wolfram’s talk at re:Clojure 2021

Wolfram Language stands out as the only production-grade programming language that’s taking meaningful advantage of modern computers to elevate programming notation beyond the static string of letters they were since the beginning of teletype terminals.

Beyond programming languages, there are many other kinds of specialized notation that would benefit from being able to be executed. Imagine if geometric diagrams, circuit layouts, and chemical reaction formulas could be “run” on the computer to become interactive or automated. If we can endow the whole universe of human notation with the strengths of programming languages like verifiability or interactivity, I think it would represent a huge jump in the way we work with knowledge as a society.

Bret Victor writes:

The very concept of a “programming language” originated with languages for scientists — now such languages aren’t even part of the discussion! Yet they remain the tools by which humanity understands the world and builds a better one.

I cannot agree more. We are still only scratching the surface of computable notation.

Part Two: Interpreting intelligence

During our discussion of notation, one frequent theme has been that better notation helps us see new ideas, or work with more complex concepts more easily. Another way to say the same thing would be that better notation raises the intellectual power we bring to a problem. To make this argument more precise, it’s worth diving deeper into intelligence itself. How can we define it, and how can we measure it?

Intelligence as run-time adaptation

The most advanced intelligence we are aware of today (that’s us, humans) emerges out of biological evolution. Intelligence and evolution are both processes of adaptation — if evolution is a “compile-time” process, where favorable genetic influences are selected for at the beginning of life, intelligence is more of a “run-time” form of adaptation, where organisms can observe and respond to their environments closer to real-time. It’s also a much more generally useful adaptation: an organism with intelligence can react to many more kinds of changes in the environment than one born with a single genetic advantage.

Paul Chiusano comments on the relationship between intelligence and evolution in his blog, where he notes

Evolution is a meta-learning algorithm that discovers its own heuristics and continually improves the rate at which it learns.

Intelligence, as a kind of real-time-reactive adaptation, is the ultimate evolutionary advantage. Intelligence can respond much faster to shifting environments than natural selection, the mechanism driving evolution.

In the short term, evolution rewards specific solutions that fit the environment, but in the long term, the trait that wins is one that lets its owners adapt quickly to any change in environment or rapidly conquer new environments. To adapt quickly to new environments requires more than strength and power and speed — it requires the ability to understand and respond to completely novel challenges that organisms weren’t pre-programmed to deal with.

This leads to our second definition of intelligence: broad generalization power.

Intelligence as generalization power

AI researcher Francois Chollet, in “On the Measure of Intelligence”, approaches the problem of measuring general intelligence by first eliminating what it cannot be. He notes that we can’t measure intelligence just by looking at how much someone or something knows, because arbitrarily large amount of training or past experience can make up for lack of intelligence. Intuitively, this is akin to saying that someone is not more intelligent than another person just because they know more information or are more skilled in a particular field. We don’t define physical fitness by a performance benchmark in a particular sport or workout, but as something that generalizes across a wide breadth of tests, including some tests that might be completely new to the athlete. He argues a similar principle should apply to measuring intelligence: we should look for a general capability across many domains, rather than good performance in one particular skill.

Within this framework, Chollet defines intelligence as generalization power. To generalize is to find abstract patterns or ideas from a few examples and apply them to new, previously unseen problems. This is what deep learning models try to do at a primitive level. But general intelligence, of the kind that humans have, can generalize much more broadly than today’s DL algorithms.

A neural net can be trained to recognize images of cars in a video feed. It can be trained to detect positive sentiment in text. To succeed at these kinds of tasks requires learning certain abstractions, like “car” or “approval” or even sub-features like “wheel” or “adjective” or “sarcasm”. From these learned abstractions, we could say the models “generalize” these ideas to new examples to perform their tasks. These kinds of systems are capable of very specific, narrow generalization within a tight domain, like “image recognition on the road” or “sentiment analysis”, but traditionally, these models have not been capable of being applied directly to related domains like face recognition or question-answering without re-training. By the definition of intelligence as generalization power, we can say more intelligent AI systems should be able to easily generalize their skill across the entire visual or linguistic domain.

With more recent transformer-based models, we are learning that better models are capable of broader generalization. The title of OpenAI’s GPT-3 paper is literally “Language Models are Few-Shot Learners” — they assert that large language models are capable of broad generalizations from few examples. Indeed, language models like GPT-3 and XLNet are generalists that can accomplish a broad range of tasks in the domain of language, from sentiment analysis to summarization to conversational dialogue. Efforts like ViT and Image GPT demonstrate that similar approaches bear fruit for the visual domain, too.

Within DL systems like this, one way to understand model performance is as a tradeoff between optimizing for past examples and optimizing for future uncertainty. One training strategy might be to learn exactly as much as needed to be able to solve examples seen during training — kind of like rote memorization. This would be maximally efficient, but the model would be ill-prepared for the future uncertainty of new and novel examples. So better training methods make careful tradeoffs — the model learns extra information and abstractions that might not be necessary now, but might prepare it to deal with the uncertainty of novel future examples. Chollet writes in the paper,

Being prepared for future uncertainty has a cost, which is antagonistic to policy compression.

This idea of trading off efficiency for generalization power leads us to our final definition of intelligence, as data compression.

Intelligence as data compression

Both of these ways of looking at intelligence

are equivalent to a third way of understanding intelligence, as data compression — the same kind of data compression we rely on to send a 4GB file across the internet in 2GB of data, or to stream 4K video over the air.

When a 1GB model learns how to recognize images from a 1TB dataset, in a way, it’s compressing the meaningful bits of information out of that 1TB dataset into a gigabyte of data. It discards random noise that seems irrelevant, and “learns” the features and abstractions that seem important for recognizing visual features in potential future examples.

To effectively compress images, a compression algorithm would be advantaged to “learn” facts about the world, like that colors are usually contiguous in images, and that the ground is often green and grassy while the sky is often white and blue. To effectively compress English text, the model might be advantaged to “learn” abstractions like common words and frequent grammatical constructs, so it can avoid inefficient, rote memorization of letters as much as possible. Learning important abstractions this way also requires forgetting information that appears useless for future tasks. I think another elegant way to understand “learning” is as a battle of compromise between the need to remember and the need to forget – when humans and AI models learn, they are both fundamentally asking, I can’t remember everything – what can I efficiently forget, so I’m best prepared for the future?

This compression-based view of intelligence has also given rise to the Hutter Prize, a prize awarded for record-setting data compression algorithms in pursuit of artificial intelligence advancements.

Part Three: Notational intelligence

In Part One, we saw that good notation helps us work with abstract, complex concepts using concrete symbols. Notation is useful because we can engage the part of our brain tuned for working with physical objects, to instead work with abstract ideas represented by physical symbols.

In Part Two, we saw that the ability to discover and work with higher levels of abstract ideas, and generalize with them broadly, is key to our intellectual ability to respond to new problems.

Taken together, I think inventing better notation is a cheap, universally useful way to increase our effective intelligence in many domains. Better notations let us work more easily with more complex abstractions, and enable us to solve new complex problems. When faced with a new seemingly intractable problem, it’s worth asking not only “What tools and discoveries might help us understand this?” but also “What notation can we use to describe this problem domain, that might help us understand this?” While better tools can help us work more efficiently or precisely with ideas we already have, better notation can enable us to imagine and discover new ideas entirely.

Humans owe much of our effective intelligence not only to our biological capabilities, but to the huge diversity and versatility of notations we bring to specific tasks. If we weren’t allowed to use Arabic numerals in math or tables in scientific literature, we’d hardly be capable of the kinds of knowledge work we do so trivially today. I think it’s critical to notice here that access to good notation amplifies our biological intelligence, and arbitrarily powerful notation can extend our capabilities into arbitrarily complex problem domains. The phrase I’ll use to refer to this idea of intelligence from the use of notation is notational intelligence.

A different way to understand the importance of notation is to conceptualize it as “input encoding” of a problem into our minds. Just as the encoding format of input is important when building machine-learned models of languages or problems like protein folding, the “encoding format” of problems for humans is also critical to our ability to understand them. There are always details about reality woven into the notations we use, whether language or mathematics. When the human brain or machine intelligence works with information expressed in a specific notation, it’s also working with a model of the world built right into the shape of the notation at hand. I’m curious if this might be a reason why complex language models appear to have a coherent model of the world, when in fact they only understand the structure of language and nothing more – language as a notation encodes so much information about the world, that a sufficiently advanced model working with the notation of language also inherently works with some half-useful model of our reality.

If inventing better notation is so critical to solving complex problems, it only makes sense to investigate how we might invent good notation, and imagine what forms it might take in the age of software interfaces. The last part of this post explores these topics.

Dynamic notation

Humans invented most notation in use today for the medium of pencil and paper, and we still work with notation in the same static way: we cross things out, we erase them, we draw up new sheets of paper (real ones from dead trees, or metaphorical ones from pixels). The way we interact with notation has been limited by the static interaction medium of paper.

Software opens us up to a much broader scope of possibilities, though. Bret Victor explains:

The purpose of a thinking medium is to bring thought outside the head, to represent concepts in a form that can be seen with the senses and manipulated with the body. (This is, for example, how paper enabled complex mathematical derivations, logical argumentation, navigation…) In this way, the medium is literally an extension of the mind.

However, static media are extremely limited in what they can conveniently represent, so much thinking is still trapped inside the head. (For example, the behavior of mathematical expressions, variable values in a computer program, connections and references between books in a library…) The dynamic medium has the potential to represent such concepts directly, to bring them out in the open, where the entire range of human faculties — all senses, all forms of movement, all forms of understanding — can be brought to bear on them.

Just as he pursues a world of dynamic media, I think we should aspire to build more dynamic notation: notation defined not only by its symbols and the way they lay out in space, but also by the way we interact with them.

Interactivity is a defining trait of computers and software as a medium, and what sets it apart from paper. But today, we interact with notation in software no differently than we interact with them on paper, which is to say we don’t interact with them much at all, beyond reading and writing them.

When games took over the computer, game designers didn’t simply simulate board games on digital screens (though that niche has its devotees) – the collision of gaming and computing spawned an entirely new field and industry dedicated to harnessing the full interactive power of software in pursuit of building ever more immersive worlds in which people could play. Yet when musicians and scientists and statisticians moved from working on paper and typewriters to working almost entirely on the computer, they simply cloned the paper medium into software. An equation in a PDF or on a website is no more immersive, interactive, or movable than ink on paper. Music notation has a more interesting story – you can write music in the standard notation in software, and most professional audio workstations or composition software will let you play it back and “execute” it, the way a programmer might execute a program. I think we can push most notations much farther along this path.

Notations are our interaction instruments for working with abstract ideas. We can’t literally grasp and manipulate abstract concepts, but we can write them down and move symbolic shadows of them around a table. How might software let us interact even more directly with our ideas? Here’s a speculative sample of possibilities:

Direct manipulation of ideas by dragging or zooming in on symbols. I want to type in the formula for gravity, and pinch in on the symbol for mass or radius to see how changes in different variables affect the overall system I’m studying. Maybe this equation can also be automatically graphed for me, and I can pinch and zoom on the graph to see corresponding changes reflected back in my equation. I want to write an outline of notes from reading a few different books, and drag and drop to move bullet points around and organize the list by different topics, by the tone of the ideas, or by how speculative different claims are.

First-class support for rich media in notation. I want to be able to copy-and-paste a vocal audio track right under the ledger lines of my song and play it back all together. When I’m reading about an architecture for a new image-processing algorithm, I want to be able to drag an image onto one end of the diagram and see how different steps in the algorithm transform the data visually. When I’m studying the mathematics of ray tracing or fluid dynamics, I want to be able to place my favorite 3D model into an equation in front of me and see normal vectors and force fields laid out before my eyes. Unlike on paper, working in the software medium lets us represent rich media like photos, 3D models, and audio faithfully. We should take advantage of it.

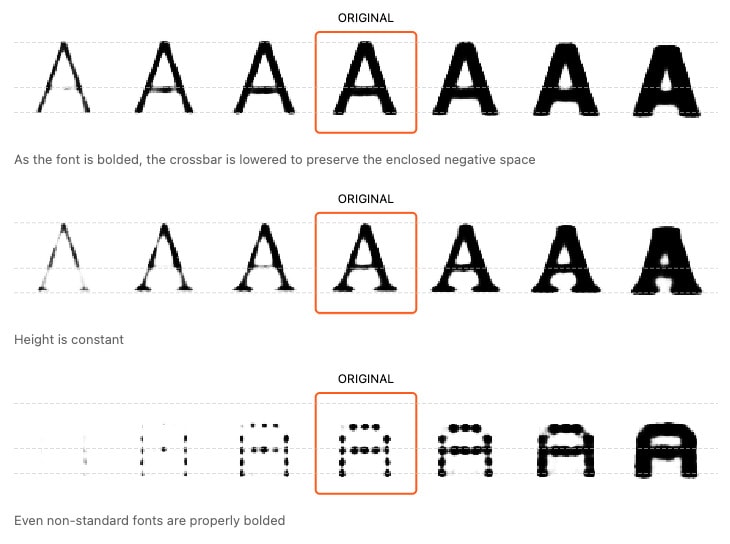
A screenshot of the publication on using generative machine learning to build machine-learned representations of qualitative concepts

– In an excerpt from the research below, we see machine-learned representations of the concept of font weight.

New notation representing abstract, fuzzy concepts quantitatively. In “Using Artificial Intelligence to Augment Human Intelligence”, the authors demonstrate how generative machine learning models can “learn” quantitative, concrete representations of fuzzy, vaguely-defined ideas like the italic-ness of a font face or the chemical instability of a particular molecular structure. I think this kind of technology, where we can quantitatively learn representations of abstract concepts, enables us to build notations for entirely new kinds of domains. How might we design a notation to describe typefaces as a composition of different styles? Could we write down formulas for chemical reactions not by explicit chemical structures, but in terms of their abstract chemical properties?

In any creative, intellectual task, there is tremendous value in being able to play with ideas, where people can explore and experiment freely without having to wait for their code to compile or their simulation to run. To make this kind of play possible in the creative workflow, the feedback loop between a what if and its implications has to be as short as possible. We shouldn’t settle for a world where we must translate lines of equations into code and paragraphs of ideas into table rows. We deserve interactive, dynamic notation, where we can play with variables in our mental models and hypotheses as easily as we move a video game character across the map.

How to design good notations

In my exploration of notations, I’ve collected some useful guidelines for designing good notation. This section is more speculative and less comprehensive than the others in the post, but I think of it as the beginning of a list of ideas that can help steer us away from the bad and towards the good as we design and extend notations.

Find a property of a concept that current notation expresses badly, and focus on expressing that more faithfully. Innovation in notation often arise out of a new way to represent some idea that was complex to express in a previous notation, or just wasn’t concretely expressed before. A trivial example is where music notation spells out chords and beats above each measure, rather than the precise notes to play. Another example from mathematics is the limit, which has a concise and precisely defined notation despite the complexity of the idea itself. Figuring out the right abstractions to realize into symbols is the key to good notation design.

A related guideline is to roll up ideas that are complex in current notation into more concise symbols. The most obvious example of this is summation (Σ) in mathematics, which wraps up a potentially infinite list of additions into a single symbol we can manipulate. In computer science, the “big O” notation embodies a nuanced idea called algorithmic complexity.

Try to express dualities in ideas that existing notations don’t suggest. For example, the union of two sets in set theory is a parallel idea to the idea of logical disjunction in formal logic. Mathematical notation for a set union looks like A ∪ B, and logical disjunction is written A ∨ B. See how they look pretty similar? The similarity in notation suggests similarity in concept. Unfortunately, most conceptual dualities like this aren’t reflected in notation. In music, F-sharp and G-flat look completely different, though they’re the same pitch (unless you’re doing some avant-garde musical experimentation). Differentiation, integration, and Riemann sums are all different views of the same idea in calculus, but their notations are nothing alike. Addition, multiplication, and exponentiation are versions of the same fundamental operation (doing some additive operation repeatedly), but they also have completely different notation. It would be interesting to design new notations that are more suggestive of these hidden relationships between ideas.

Notation doesn’t have to look like language, or like symbols on a horizontal line. As we imagine new kinds of notation, it’s easy to get stuck in a status quo bias, thinking within the set of things we can type into a computer and look and feel like language or math. I think we should be aware of the risk of falling into this trap, and actively imagine non-linguistic notation that take better advantage of two- or three-dimensional, interactive capabilities of software. For example, in digital audio workstations for music production, tracks aren’t expressed using notes on ledger lines like parts in traditional music notation. Instead, tracks are visualized so that they can shrink and expand to reveal detail or high-level shape as the musician moves around the software interface. This interface represents a new kind of notation for music, one that provides unique benefit in an interactive interface.

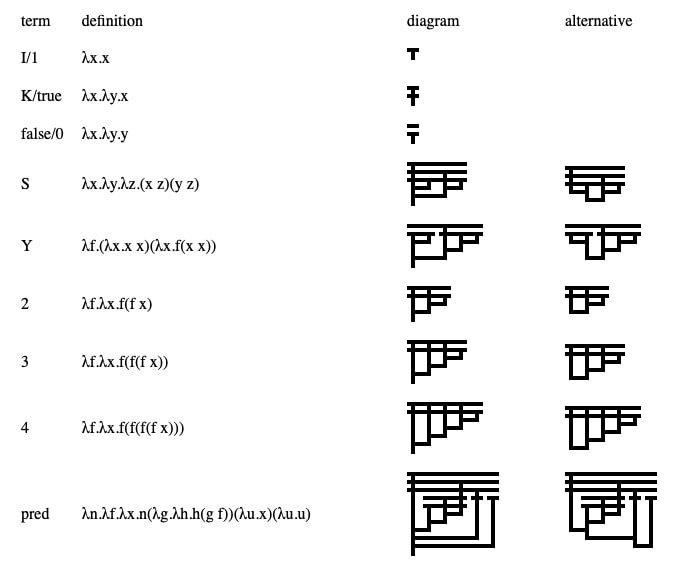
Geometric diagrams representing functions and expressions in the lambda calculus

– Notation doesn’t have to look like language. (Taken from “Lambda diagrams”)

Whatever the exact form, future notations native to the software medium will depart often from its static predecessors, only rhyming with history where it’s useful.

Future directions

Throughout the post, I’ve highlighted two promising paths for augmenting our thinking and creativity with better notation.

  1. Improving our existing notation to be more interactive and dynamic
  2. Inventing new notation to let us work quantitatively with more abstract ideas

Though it’s early, I want to end with some of my thoughts on what future work in this direction might look like.

One path I’m beginning to investigate is notation for working with complex networks of ideas. I explored the diversity of domain-specific notations in this post, like music notation or regular expressions, but the most common, versatile, and intuitive notation is still natural language. How can we improve the way we work with written language to be more interactive and dynamic?

Complex ideas often present themselves as densely connected networks of smaller ideas. In light of this structure, I think a good dynamic format for documents should help readers and writers explore these graphs of ideas intuitively. Perhaps we can make effective use of the human brain’s finely tuned ability to navigate physical spaces, and construct documents that feel like “spaces” that we read by “navigating” it. Rather than having “notes” that are just collections of homogeneous chunks of text, maybe notes can take on different roles in this map of ideas – some notes are more “paths” that help us discover other notes; some notes are more “districts” that act as topic-level containers, and some notes are “landmarks” that go deep into specific concepts.

There are also worthwhile sources of inspiration elsewhere: Within the world of software development, we’ve invested decades of effort into graph-exploring interfaces, too, called code editors. Source code is often graph-shaped, and I think many of the ideas that apply to navigating complex codebases would be equally fit for navigating complex webs of ideas.

Lastly, I want to investigate ways to make written language itself more dynamic. What if we could ask a paragraph discussing an abstract idea to produce examples of its own argument? What if you could turn a dial on any article or blog post from “1-minute summary” to “book-length treatise” to get exactly the depth and brevity you want to spend on a topic? In the same way we can manipulate numerical models in Excel, I want to imagine dynamic documents where I can extend and stretch ideas expressed in prose with the help of software. I want my notes to self-organize into topics and lists based on the context of my current thought. When we dream of interactive notation for thought, I think these kinds of interactions should be our starting place.

Another important open question in this space concerns measuring our progress. Once we have experiments and prototypes for better notation, how might we measure our success? What makes new notation valuable?

The value of notation lies in how it enables us to work with new abstractions. With more powerful notation, we can work with ideas that would have been too complex or unwieldy without it. Equipped with better notation, we might think of solutions or hypotheses that would have been previously unthinkable. Without Arabic numerals, we don’t have long division. Without chess notation, the best strategies and openings may not have been played. Without a notation for juggling patterns called Siteswap, many new juggling patterns wouldn’t have been invented.

Right now, today, we can’t see the thing, at all, that’s going to be the most important 100 years from now. – Carver Mead

I think notation should be judged by its ability to contribute to and represent previously unthinkable, un-expressible thoughts.

A notation is not a single feature or symbol. Innovation in notation and dynamic documents won’t arrive as a single big idea or a single product from a new startup. Just as mathematical notation isn’t just the Σ sign or the concept of using a letter in place of numbers, the revolution we seek won’t be just bidirectional links or just spatial interfaces or just GPT-whatever. As generations of companies and products come and go touting new ideas and interaction mechanics, we shouldn’t ask “Does this product finally get it right?” but rather “What good ideas can we take from this to our vision of better notation, better documents, and better ways of working with ideas?”

There’s a subtle but important distinction between augmenting human productivity, which is every tech company’s aim, and augmenting human intellect. The former is an economic endeavor that helps us accomplish more of what we could do already; the latter is a step towards helping us invent new things and see new ideas we could not before. In the path to build newer and better tools, we should not be blind to the fact that the future has always been defined by nascent ideas – ideas that may be written in words we don’t recognize yet and symbols that may not yet exist. It is up to us to ensure that by the time the world needs those ideas, we can speak of them, write them down, and pass on the knowledge.

← Towards a research community for better thinking tools

Navigate, don't search →

I share new posts on my newsletter. If you liked this one, you should consider joining the list.

Have a comment or response? You can email me.